Wavelets ? A practical overview

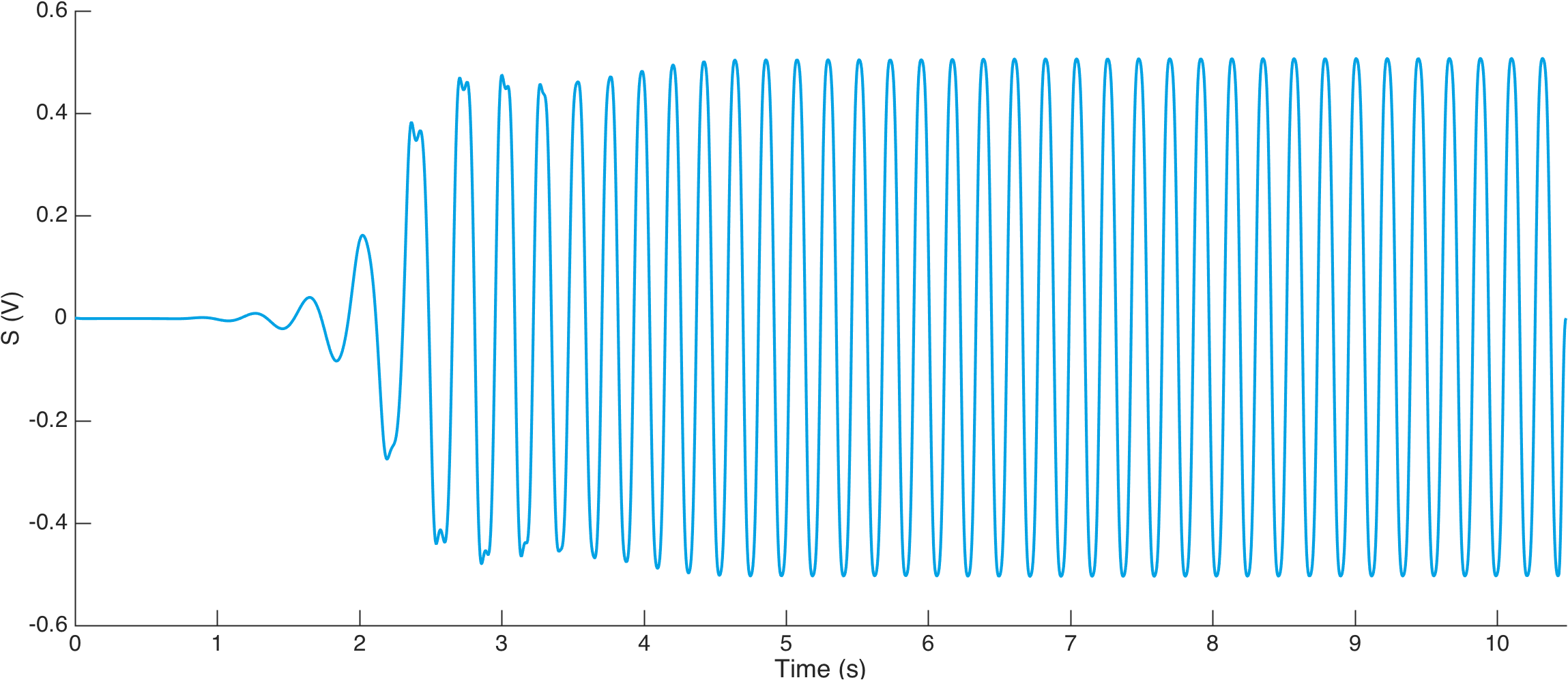
The following instance perfectly illustrates the possibilities offered by wavelet time-frequency analysis to extract main features hidden in weak signal components and whose Fourier analysis can hardly reveal. The signal considered here is a digital record of a clarinet sound that was rescaled in time and whose time response is populated with repeated oscillations likely to be related to a stationnary frequency. In other words, the sound happens to be a single note of music that was played during quite a long period of time. 
A display of the Fourier power spectrum of the clarinet signal clearly indicates the occurrence of two frequency peaks

• first peak f0 = 4,9 Hz stands for the fundamental frequency of the note
• second peak f3 = 13,7 Hz is the 3rd harmonic of the note

Fourier spectrum also vaguely highlights a continuous and low energy frequency bandwith below frequency f0. These spectral information are possibly correlated with some small fluctuations noticeable at the beginning of sound but it is impossible to say more about it by using Fourier analysis.

The scalogram of clarinet sound computed with the Meyer wavelet permits to explore the sound dynamics with a brand new glance. Sound energy happens to be mainly localized in two clusters within different frequency bands

• a first cluster in red arises at the beginning of the note in a time-frequency area neighbouring f0=4,9 Hz and lives as as long as the note is played 
• a second cluster in blue starts one second after the note in a frequency band surrounding f3=13,7 Hz and its energy rapidly vanishes after time 3,5 seconds

Multiresolution properties of the wavelet analysis that was used moreover enable to numerically perform a closer zoom on signal time-frequency events. Here it literally permits to dive at the heart of sound signal to reveal the occurrence of a third cluster with very low energy surrounding the second harmonics f2=9,8 Hz of the played note.

A crazy climber algorithm was used to calculate the ridges of wavelet clusters that concentrate most of the energy of clusters and that permit to follow the time-evolution of instantaneous frequencies of the sound components 

• frequency of the ridge of the first cluster starts above 2,2 Hz at the beginning of sound then gradually increases  similarly like a chirp signal before stabilizing on the fundamental frequency f0=4,9 Hz of the note
• the ridge of the second cluster starts a little bit later and climbs from above 8Hz till frequency f3=13,7 Hz before almost vanishing due to a lack of energy

Wavelet analysis stresses a migration of frequencies f0 and f3 at the beginning of the played note which may physically be interpreted by the energy activation of some transient sound nonlinearities often referenced as the attack of the note. Diving deeper into the sound would almost surely reveal a similar phenomenon for the second harmonic at even lower energy levels. This practical case highlights one of the countless possibilities offered by wavelet analysis to extract the main information of complex transient signals.