Wavelet analysis consist in making a local comparison of a signal with wavelet patterns similarly like a mathematical microscope that permits to zoom on signals with various scaling magnification.

Wavelet analysis is performed by a mathematical transform which stands for a convolution between the investigated signal and shifted to a position b and dilated by a scale a patterns of a mother wavelet. One finally obtains a two-dimensional mapping built over the time-frequency plane (a,b)

By means of an admissible condition on the wavelet, the transform is reversible and makes it possible to reconstruct the signal from the synthesis formula


Wavelet analysis is performed by a mathematical transform which stands for a convolution between the investigated signal and shifted to a position b and dilated by a scale a patterns of a mother wavelet. One finally obtains a two-dimensional mapping built over the time-frequency plane (a,b)

By means of an admissible condition on the wavelet, the transform is reversible and makes it possible to reconstruct the signal from the synthesis formula

Effect of shift-dilation in Fourier domain
Operations of shift and dilation of a function defined in the physical space have their counterpart in their Fourier space
- shifting of an offset b

- dilation of a scale a

- shift-dilation combined (a,b)

The representation of the shifted-dilated pattern of the wavelet in the time-frequency plane is of particular interest

The transformation imagined by J. Morlet allows to pave the whole of the time-frequency plane by choosing adapted couples (a, b). This property makes it possible to make an analogy with the optical microscope that is the transform that allows to zoom inside a signal
- at a position given by the focal distance b
- with a given magnification proportional to 1/a
- the lens of the microscope being given by the choice by the wavelet
Discrete wavelet transform
A result given by I. Daubechies makes it possible to demonstrate that a discrete network of points (aj,bk) of the time-frequency plane is sufficient to reconstruct a signal from the knowledge of its wavelet transform calculated on the dyadic grid. Graphically the transition from the continuous to the discrete is symbolized by the following diagram


The discrete wavelet transform thus returns to spanning a signal by using a series of wavelets whose coefficients are given by
- analysis: wavelet coefficients

- synthesis: wavelet series

In the case of a smooth signal, its related wavelet series is advantageously lacunary.
Wavelet scalogram
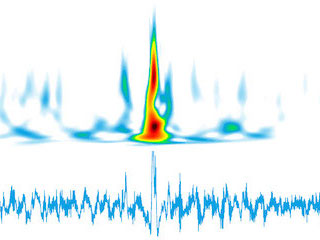
It becomes possible to visualize the "wavelet" energy of a given signal by adopting the scalogram representation which consists in drawing the isocontour lines of the wavelet field calculated on the dyadic grid. Following the theory of wavelet frames, Letscan has developed the innovative concept of super-resolution wavelet analysis which allows to fastly and efficiently analyze the instantaneous frequencies of a signal spanned onto dense dyadic grids of the time-frequency plane with adaptive zoom capabilities.


An instance is given by analyzing a signal that contains transient information. The scalogram shows a succession of clusters whose ridges concentrate essential information on the instantaneous frequencies of the signal.


 English (UK)
English (UK) Français (FR)
Français (FR)